What is the resistance of a square laminar when measured from the corners? More precisely, assume you have a square slice of material with conductivity σ of side length L and thickness τ ≪ L. If you connect an ohmmeter between two diagonally opposite corners, what resistance will you measure?
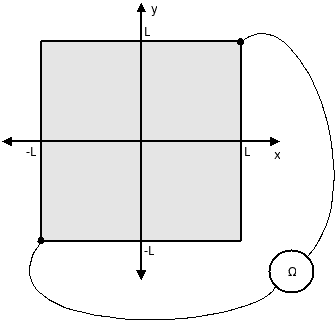
Position the slab of material so that it occupies the space [-L,L]⨉[-L,L]⨉[-τ,τ]. We will connect the contacts of the ohmmeter to the vertical edges x=y=-L and x=y=L. Let V(x) be the electrostatic potential and E = -∇V be the electic field. According to Ohm's law, the current density is J = σE.
Since there is no net charge density in the material, the potential obeys the Laplace equation:
∇2 V = 0.
No current can flow past the material boundaries. This gives the boundary condition
dV/dn = 0, when x=±L, y=±L or z=±τ,
where dV/dn is the derivative of the potential in the direction of the face normal.
The resistance is a ratio R=ΔV/I. Therefore, we can assume that there is a constant potential difference across the terminals. This gives another boundary condition:
V(-L,-L,z) = -1 and V(L,L,z) = 1.
Given V(x), we can calculate the current through the material:
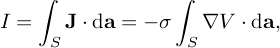
where S is a surface inside the material enclosing (-L,-L,z). The resistance is then given by R = 2/I.
The first problem then is to solve for V(x). Some observations:
The equipotential curves are perpendicular to the edges due to the first boundary conditions. It's easy to sketch a qualitative solution:
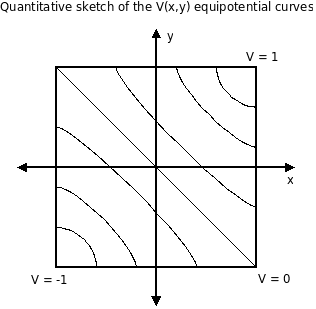
I found this problem in [1]. There, they calculated the resistance to be R = 4/π 1/(τσ) using an infinite number of image charges. However, I want to check this answer numerically.
[1] Lawrence R. Mead, Resistance of a square lamina by the method of images, American Journal of Physics, 77 (3), (2009). Abstract