A discrete version of the divergence theorem

2009-06-20

The divergence theorem (Gauss's theorem) from vector calculus says

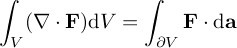
I am interested in the case where the vector field is derived from a scalar potential F = ∇u:

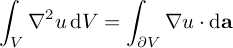
This theorem is for a continuous system in ℝ³. However, numerical algorithms often operate on discrete grids in ℤ^d where d = 2 or 3. I will now derive a discrete version of this theorem.

Definitions:

Let u be a scalar field on the grid u: ℤ^d → ℝ, x ↦ u_x.

Let x, y ∈ ℤ^d. We'll use the Manhattan metric |x - y| = Σ_i |x_i - y_i|. Cells x and y are called adjacent if and only if |x - y| = 1. Note that diagonal cells are not adjacent.

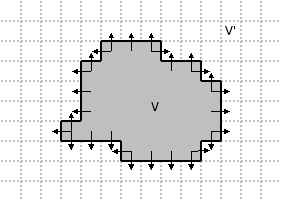
Let V be a subset of ℤ^d. V' is the complement of V in ℤ^d.

Let n_x be the number of cells adjacent to x in V. Therefore, n_x = Σ_{y∈V, |x-y|=1} 1.

Let the second-order finite difference Laplacian be given by L_x = - 2d u_x + Σ_{y, |x-y|=1} u_y.

Theorem

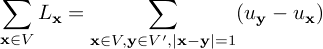
Note that right-hand side involves only points on the boundary of V. These correspond to first-order finite difference derivatives. There is one term for each arrow in this diagram:

Proof

Starting from the left-hand side, expand the Laplacian to get a sum of field terms:

Σ_x∈V L_x = Σ_x c_x u_x,

where c_x are constant coefficients. From the definition of the Laplacian, we can see that c_x = n_x - 2d if x∈V, or c_x = n_x if x∈V':

= Σ_x∈V u_x (n_x - 2d) + Σ_x∈V' u_x n_x. (1)

Since each cell is adjacent to 2d others,

2d = Σ_{y, |x-y|=1} 1
= Σ_{y∈V, |x-y|=1} 1 + Σ_{y∈V', |x-y|=1} 1
= n_x + Σ_{y∈V', |x-y|=1} 1
2d - n_x = Σ_{y∈V', |x-y|=1} 1.

Now put this into (1):

Σ_x∈V L_x
= - Σ_{x∈V, y∈V', |x-y|=1} u_x + Σ_{x∈V', y∈V, |x-y|=1} u_x
= Σ_{x∈V, y∈V', |x-y|=1} (u_y - u_x). ■